
Don't worry, you'll see what I mean in the next article. Lets orient each of the three pictured surfaces so that the light side is considered to be the positive' side. Edit: In Cartesian coordinates, we have F N 3 ( x2 + y2) 2a2 a and dS a a2 x2 y2dxdy.
3d flux integral how to#
Thus, the surface integral over the half-sphere for z > 0 is. Calculus 3 tutorial video that explains how to calculate flux across a curve using a line integral of a vector field.

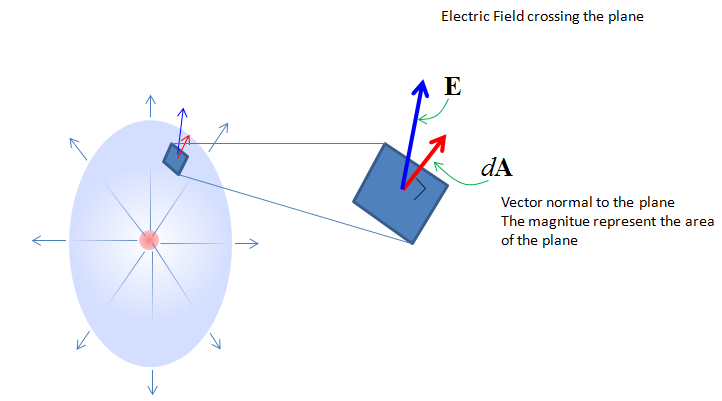
Flux integrals deal specifically with oriented surfaces. It depends on which part of the surface you consider to be oriented in which direction and this is an arbitrary choice. ∮ C F ⋅ n ^ d s = ∫ 0 2 π F ( r ( t ) ) ⋅ ⏟ Velocity at a point n ^ ( r ( t ) ) ⏞ Normal vector at a point ∣ ∣ r ′ ( t ) ∣ ∣ d t ⏟ d s = ∫ 0 2 π ( ⋅ ) ∣ ∣ ∣ ∣ d t = ∫ 0 2 π ( ⋅ ) ∣ ∣ ∣ ∣ d t = ∫ 0 2 π ( 9 cos 3 ( t ) + 3 sin 2 ( t ) ) 3 2 sin 2 ( t ) + 3 2 cos 2 ( t ) d t = ∫ 0 2 π ( 9 cos 3 ( t ) + 3 sin 2 ( t ) ) 3 sin 2 ( t ) + cos 2 ( t ) ⏟ = 1 d t = ∫ 0 2 π ( 9 cos 3 ( t ) + 3 sin 2 ( t ) ) 3 d t = 9 ∫ 0 2 π ( 3 cos 3 ( t ) + sin 2 ( t ) ) d t \begin C start color #bc2612, C, end color #bc2612 itself, since that's all you need. The corresponding surface element on the sphere S: x2 + y2 + z2 a2 is. The total flux is just guaranteed to be zero is all. v t e In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces.


 0 kommentar(er)
0 kommentar(er)
